
Este é o segundo exemplo da série de exercícios resolvidos ensinando como fazer diagrama de força cortante e momento fletor em viga engastada. E pra esse caso em específico vou resolver o exercício de viga Gerber.
Observe que a figura apresentada é uma viga engastada no ponto "A", pinada no ponto "B" e apoiada no ponto "C". Sobre a viga está um carregamento distribuído de 20kN/m, vou calcular as reações nos apoios e fazer os diagramas de força cortante e momento fletor.
1° Passo: fazer o diagrama de corpo livre indicando as reações dos apoios e as forças resultantes do carregamento.
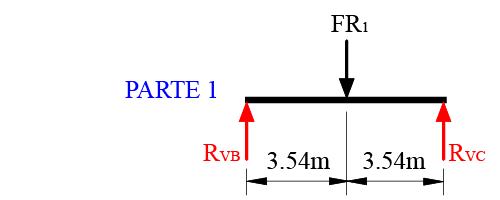

Veja que a barra foi dividida em duas partes, onde a parte 1 compreende do ponto B até o ponto C e a parte 2 do ponto A ao ponto B.
RHA = Reação Horizontal no Apoio A
RVA = Reação Vertical no Apoio A
RVB = Reação Vertical no Pino B
RVC = Reação Vertical no Apoio C
MA = Momento do Apoio A
2° Passo: Calcular as forças resultantes do carregamento.


3° Passo: Calcular as reações dos apoios. Vou aplicar as equações do equilíbrio estático para encontrar as reações.
Para a parte 1 da viga vou resolver por análise. Observe que a força resultante está bem no centro da viga, isso significa que metade da força resultante está para RVB e a outra metade da força está para RVC. Portanto podemos dizer que RVB é igual a RVC que é igual a força resultante 1 dividido por dois.

Para a parte 2 da viga vou aplicar as equações do equilíbrio estático para calcular as reações dos apoios.
Somatória dos momentos igual a zero considerando sentido de giro horário positivo.



A reação horizontal no apoio "A" será igual a zero.
Agora que as forças de reação foram encontradas vou para os passos de como calcular as forças internas e fazer os diagramas de força cortante e momento fletor.
4° Passo: Cortar a viga Gerber nos pontos S1e S2 indicado na figura abaixo.
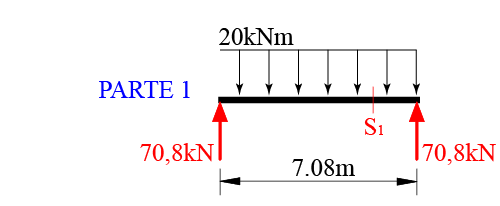

5° Passo: Montar o diagrama de corpo livre indicando as forças internas desenvolvidas nos cortes S1e S2 e a força resultante do carregamento.
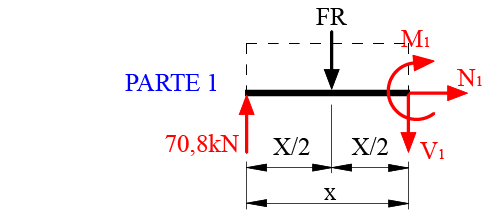
Observe que no corte S1 foi incluso as forças N1 (Normal), V1 (cisalhamento) e M1 (Momento Fletor) e no corte S2 foi incluso as forças N2 (Normal), V2 (cisalhamento) e M2 (Momento Fletor).
A força resultante deverá ser calculada conforme abaixo.
Agora, no próximo passo vou aplicar novamente as equações do equilíbrio estático e encontras as funções que descrevem as forças internas na viga.
6° Passo: Calcular as forças internas nos pontos das vigas.
Parte 1 da viga, ponto S1
Somatória dos momentos no ponto S1 igual a zero, considerando sentido de giro horário positivo.


Somatória das forças verticais no ponto S1 iual a zero, considerando sentido para cima positivo.

Somatória das forças horizontais no ponto S1 igual a zero, considerando sentido para direita positivo.

Parte 2 da viga, ponto S2
Somatória dos momentos no ponto S2 igual a zero, considerando sentido de giro horário positivo.

Somatória das forças verticais no ponto S2 igual a zero, considerando sentido para cima

Somatória das forças horizontais no ponto S2 igual a zero, considerando sentido para direita positivo.

7° Passo: Resumo das forças internas que atuam nos pontos S2 e S2 da viga.

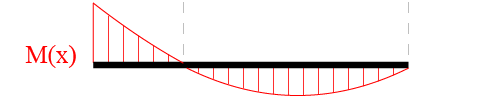
8° Passo: Traçar o diagrama de força cortante e momento fletor para a viga, respeitando as equações apresentada no resumo acima.


Quer aprender através de exercícios resolvidos em vídeos com um professor?, assista a apresentação agora >> CLIQUE AQUI <<







Muito bom, explicou passo a passo, muito obrigado
ResponderExcluir