Diagrama de Esforço Cortante e Momento Fletor Passo a Passo

Este artigo tem o objetivo de lhe ensinar como fazer o diagrama de esforço cortante e momento fletor passo a passo. Para este exemplo separei um exercício do livro de Estática do Hibbeler.

O problema diz o seguinte: trace os diagramas de forças de cisalhamento e de momentos fletores para a viga (a) em termos dos parâmetros mostrados; (b) considere que P = 600 lb, a = 5 pés, b = 7 pés. (Fonte: Hibbeler, R.C. Estática: mecânica para engenharia, vol. 1).

Neste artigo vou resolver apenas a parte (b) do problema.

Antes de fazer o diagrama de esforço cortante e momento fletor passo a passo é preciso saber qual a intensidade das forças de reação dos apoios. Então, o primeiro passo será fazer o diagrama de corpo livre da viga.

Diagrama de esforço cortante e momento fletor passo a passo: Passo 01, fazer o diagrama de corpo livre da viga.

Veja na imagem acima que no lado esquerdo da viga possui duas reações, uma na direção vertical (RVA) e outra na direção horizontal (RHA). Já no lado direito possui apenas uma reação vertical (RVB). Isso acontece porque o apoio esquerdo é do tipo fixo e o direito é do tipo simples. Se você não sabe nada sobre apoios, veja o artigo Tipos de Apoio Em Estruturas.

Diagrama de esforço cortante e momento fletor passo a passo: Passo 02, calcular a intensidade das forças de reação dos apoios.

Para calcular as reações dos apoios é necessário usar as equações do equilíbrio estático, fazendo a somatória das forças verticais, horizontais e os momentos que atuam sobre a viga. Lembre-se, para esses cálculos é preciso escolher um ponto de referencia e arbitrar os sentidos das forças, nesse exemplo usarei como referencia o apoio “A”.

Somatória de momentos no ponto “A” igual a zero. Sentido de giro horário como positivo.

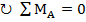
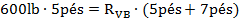
Somatória das forças verticais igual à zero. Sentido para cima positivo.

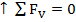
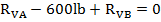
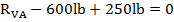
Somatória das forças horizontais igual à zero. Sentido para direita positivo.

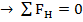
Observe que a força de reação horizontal é igual à zero, pois não há nenhuma outra força sendo aplicada nessa direção além de RHA.

Diagrama de esforço cortante e momento fletor passo a passo: Passo 03, dividir a viga em seção para encontrar as forças internas.

Ao cortar a viga em um ponto qualquer, nesse ponto de corte surgem as forças internas que são chamas de: força normal (N), força cortante (V) e momento fletor (M). O foco dessa resolução é traçar o diagrama de esforço cortante e momento fletor.

Para esse problema, é preciso cortar a viga em dois pontos. O primeiro corte será entre as forças de 350lb e 600lb, chamarei de S1. O segundo corte será entre as forças 600lb e 250lb, chamarei de S2.

A imagem abaixo ilustra os pontos onde serão feito os cortes na viga.

Tanto no ponto S1 quanto no ponto S2 surgem o esforço cortante e momento fletor que será calculado adiante.

Diagrama de esforço cortante e momento fletor passo a passo: Passo 04, calcular a intensidade das forças internas no ponto S1.

A figura acima representa a viga cortada no ponto S1, após efetuar o corte três forças aparecem na parte interna da viga, são elas: força normal (NS1), força cortante ou de cisalhamento (VS1) e momento fletor (MS1). Todos os sentidos das forças internas indicados acima são arbitrário, você pode escolher qual achar melhor, eu escolhi esses.

Agora é só encontrar a intensidade das forças internas no ponto S1 e para isso basta aplicar as equações do equilíbrio estático conforme apresentado abaixo

Somatória de momentos no ponto “S1” igual à zero. Sentido de giro horário como positivo.

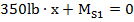
Somatória das forças verticais igual à zero. Sentido para cima positivo.

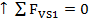
Somatória das forças horizontais igual à zero. Sentido para direita positivo.

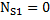
Diagrama de esforço cortante e momento fletor passo a passo: Passo 05, calcular a intensidade das forças internas no ponto S2.

A figura acima mostra a viga cortada no ponto S2, basta aplicar as equações do equilíbrio estático para calcularmos os esforços internos nesse ponto.

Somatória de momentos no ponto “S2” igual à zero. Sentido de giro horário como positivo.

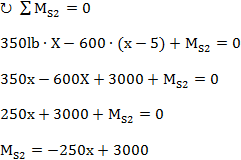
Somatória das forças verticais igual à zero. Sentido para cima positivo.

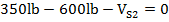
Somatória das forças horizontais igual à zero. Sentido para direita positivo.

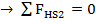
Diagrama de esforço cortante e momento fletor passo a passo: Passo 06, resumo das forças internas da viga.

Listar de forma resumida e organizada todos os cálculos das forças internas feitos anteriormente é bom para facilitar quando for fazer o diagrama de esforço cortante e momento fletor.

Observando abaixo, podemos desconsiderar o diagrama de força normal porque é nulo.

N       V          M

S1 0        350lb 350x

S2       0       -250lb -250x+3000

No momento fletor, o “x” representa a distância. Para saber qual a intensidade do momento fletor em um ponto qualquer da viga basta substituir a distância do ponto na equação do momento fletor.

Diagrama de esforço cortante e momento fletor passo a passo: Passo 07, traçar os diagramas.

Espero ter ajudado você a aprender fazer Diagrama de esforço cortante e momento fletor passo a passo.